As a pattern junkie, you may know how to capture the structure of a repeating pattern in a diagram; that is, determine to which of  the seventeen symmetry types a pattern belongs. Yes, we are talking about surface patterns, or wallpaper patterns, whose type is determined by what mathematicians call the plane (2D) symmetry groups. Turns out all pattern schematics are not made equal and, surprisingly, the most simple diagram, which is also the most useful for the non-mathematically inclined, is also the least known or, we might even be tempted to say, a well-kept secret.

Traditionally, because you are dealing with symmetries, your pattern schematics would show symmetry operations, probably combined with boundaries of repeating units (“unit cells” or “fundamental domains”), and often made more intelligible by superimposing  actual patterns produced by a simple asymmetric bit (a line, a comma, or a letter of an alphabet). Here are a few examples of the standard approach, which we show mostly to help you fully appreciate a simpler one that’s coming up next:

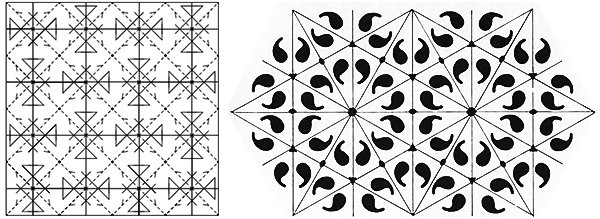
There’s no shortage of references that introduce pattern diagrams, starting from Wikipedia and including articles by Baloglou, Bart and Clair, and Bar-Natan, to name just a few.

As symmetry schematics get complicated rather quickly, one might settle on a representative icon for each symmetry type and jam all the 17 icons into a small space, as proven useful in the Artlandia symmetry panel:

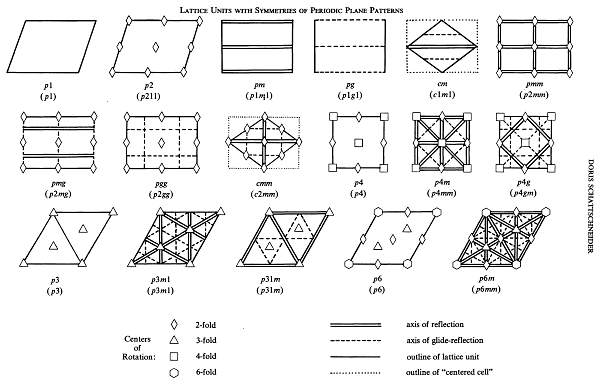
But if we set out to find the simplest ever schematics, the prize has to be awarded to Andreas Speiser, who studied the general group theory and in that context looked  into how symmetry operations combine to produce ornaments. The following schematics are cited from the 1937 edition of his book Die Theorie der Gruppen von Endlicher Ordnung:

This unpretentious diagram is unbeatable in its simplicity. You will notice how skillfully Speiser puts straight line segments to play up reflection axes, adds smallish ticks to highlight rotations—or longer ticks to emphasize reflections or glide reflections—and in so doing gives the schematics its altogether unmistakable look.

Feel free to download a vector form of Speiser’s diagram. If you are a SymmetryWorks user, you will also be able to experiment with the patterns and see how they are constructed.

And, as a side note, isn’t it amazing that a modestly small number of symmetry types rule the whole wondrous universe of repeat patterns, including masterpieces by Morris and Escher and countless other famous and anonymous pattern designers, from the earliest tribes to the Egyptians, Greeks and Romans, to modernity.

Luckily, a modern-day Morris or Escher would not need to be concerned with the tedium of performing thousands of precise symmetry operations. That part of the job is conveniently farmed out to specialized pattern design software (also called pattern design CAD systems), such as SymmetryWorks, SymmetryShop, or SymmetryMill, which produce any type of symmetry at a single click on the symmetry panel. So you, the designer, can concentrate your efforts on a single repeating unit (motif) and immediately see how the motif instances interplay when they come together in a pattern. And then the simple pattern diagram in this post can save you some unnecessary trial and errors when choosing symmetry for the pattern structure you have in mind. And it’ll help you to grasp the underlying structure when you happen on an interesting pattern by accident, which is not at all rare when another symmetry is just a click away.

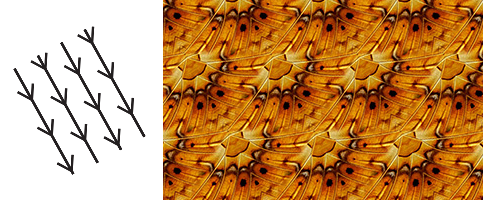
Here are some more examples of each symmetry type, in the same order, in case you wish to train your eye on Speiser’s diagrams:

And back to the title of this post, we challenge you to find or come up with an even simpler illustration of 17 pattern types. Let us know if you succeed! Until then the Speiser diagram will hold the grand title of The Simplest Pattern Diagram On The Web.

Last updated: September 3, 2017